Argument mapping

Argument maps are colored box-and-arrow diagrams that represent the logical structure of arguments in natural language. The best way to explain how argument mapping works is by providing an example. Argument mapping can be used to represent all sorts of content, but as I am a philosopher, let us consider a philosophical argument. This one is drawn, with a bit of revision, from a passage by Lucretius, the Roman poet and Epicurean philosopher.

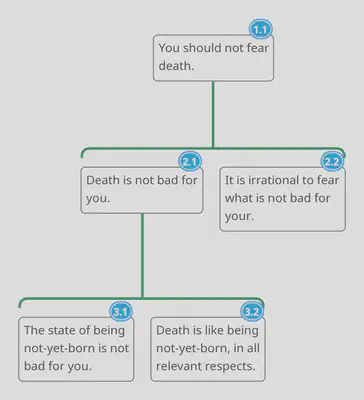
“The state of being not-yet-born is not bad for you. But being dead is just like being not-yet-born, in all relevant respects. Death, therefore, is not bad for you. And since it is irrational to fear what is not bad for you, you should not fear death.”

The conclusion of this argument is given in the final five words. To create an argument map, we extract the conclusion, place it at the top of an inverted tree-structure, and then arrange the supporting claims beneath it.

This is a simple map of a simple argument. Once you’ve had an opportunity to inspect the map, it may seem obvious that it accurately represents the logical structure of the argument. However, the process of figuring out how to produce this map is neither automatic nor trivial. Even after a few weeks of practice, producing a simple map like this requires significant effort, and produces a correspondingly significant increase in the degree to which students understanding the reasoning involved.